What is the Birthday Problem aka Birthday Paradox?

First of all,it is not really a parado Suppose you are attending a party. How big do you think the party has to be in order to be that there are two people in the party with the same birthday? Assume, every birthday is equally likely

#collapse-hide
x = int(input("Put your guess in here:"))
if x < 23:
    print("Too low..wow your intution is wrong on the opposite way than most people XD")
elif x > 23:
    print("That's too high,read on to find out why")
else:
    print("Perfect,You have seen this problem before haven't you?")

Put your guess in here:185
That's too high,read on to find out why

The math (stuff that goes over my head on the first read):

Let 'n' be the number of people at party.

Let's assume that everyone in the party has a different birthday.

What is the probablity 'q' of that happening?

if n = 2:

number of choices for first birthday,b1 = 365
number of choices for second birthday,b2 = (365 - 1) = 364 (Anything other than first birthday)

probablity of choosing the particular day as first birthday = 1/365
probablity of choosing the particular day as second birthday = 1/365 
reason: probablity of choosing any number from 365 choices = 1/365

q(n = 2) = (365 x (1/365)) x ((364) x (1/365)) = 364/365

if n = 3:

similarly,

    b1 = 365
    b2 = 365 - 1 = 364
    b3 = 365 - 2 = 363 (anything other than 2 already choosen)

q(n = 3) =  (365 x (1/365)) x ((364) x (1/365)) x (363 x (1/365)) = (364 x 363)/(365 x 365)

hence:

q(n) = (364 x 363 x 362 x .... (365 - (n - 1))) / (365)^(n - 1)
     = (365!)/ ((365^n) x ((n - 1)!))

The above calculates the formula for party of 'n' people all with unique birthday.

Now the only two scenarios possible are :

either there is some birthday match or there is none

By law of total probablity: p(n) + q(n) = 1 where, p(n) is the probablity there is a birthday match therefore: p(n) = 1 - q(n)

Using the above formulas,the

#collapse-hide
def q(n, choices = 365):
    q = 1
    for i in range(1, n):
        x = (choices - i)/choices
        q *= x
        
    return (q) #at max it is 1


#collapse-hide
def p(n, choices = 365):
    return(1 - q(n,choices))

Probablity of your guess (in %):

note: Python tends to approximate 99.99999... to 100

#collapse-hide
print("p(x):",100 * p(x))
print("q(x):",100 *q(x)) #for higher guesses comes to 100 because 99.99999

p(x): 100.0
q(x): 1.1819355706789237e-23

Probablity at 23: 

(The magic number)
If you reverse the above calculation the number that is closest for 50% is 23

#collapse-hide
print("p(23):",100 * p(23))
print("q(23):",100 *q(23))

p(23): 50.729723432398565
q(23): 49.27027656760144

It still isn't believable, simulate it:

Why is (most of the time) our guess is too high?

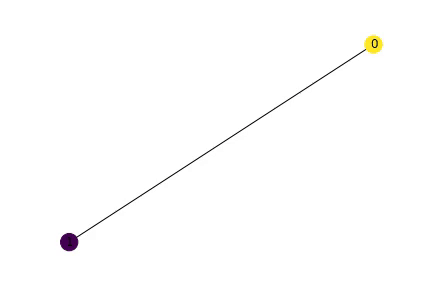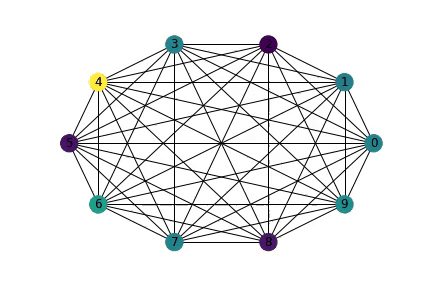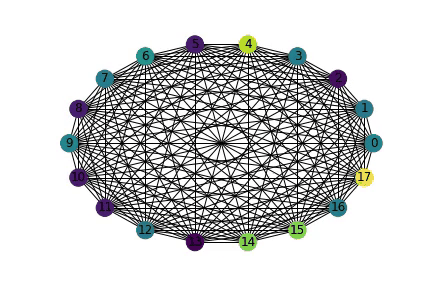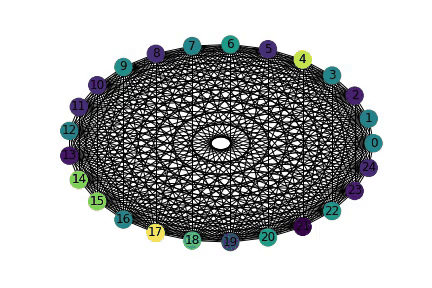
As, the number of people grow linearly : n (i.e 1,2,3,4,5,6,..) the number of pairs grow quadratically : (n x (n - 1)/2) (i.e 0,1,3,6,10..) The animation below shows how the "pairs" (representated by edges increase) as number of people (representated by nodes) increase

#collapse-hide
#imports
import random
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.animation
from moviepy.editor import *


#collapse-hide
#intializations
birthdays_possible = 365
X = nx.Graph()
X.add_node(0)
birthdays = [random.choice(range(birthdays_possible))]
match = list()
fig, ax = plt.subplots(figsize=(6,4))
plt.close()


#collapse-hide
def update(num):
    ax.clear()
    if num > 0:
        birthdays.append(random.choice(range(birthdays_possible)))
    print(birthdays)
    for i in range(num):
        X.add_edge(i,num)
        if birthdays[i] == birthdays[num]:
            match.append('r')
        else:
            match.append('k')
    nx.draw_circular(X, ax = ax, with_labels = True, node_color = birthdays,edged_color = match)


#collapse-hide
ani = matplotlib.animation.FuncAnimation(fig, update, frames= 25, interval= 2000, repeat=True)


#collapse-hide
print("birthdays selected in the animation:")
ani.save('birthday.mp4')

birthdays selected in the animation:
[7]
[7]
[7, 27]
[7, 27, 18]
[7, 27, 18, 182]
[7, 27, 18, 182, 222]
[7, 27, 18, 182, 222, 295]
[7, 27, 18, 182, 222, 295, 222]
[7, 27, 18, 182, 222, 295, 222, 278]
[7, 27, 18, 182, 222, 295, 222, 278, 128]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18, 360]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18, 360, 63]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18, 360, 63, 115]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18, 360, 63, 115, 219]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18, 360, 63, 115, 219, 158]
[7, 27, 18, 182, 222, 295, 222, 278, 128, 343, 185, 342, 110, 258, 217, 147, 300, 203, 18, 360, 63, 115, 219, 158, 242]


#collapse-hide
def is_there_a_match(birthdays):
    return (len(birthdays) != len(set(birthdays)))


#collapse-hide
is_there_a_match(birthdays)

True

#collapse-hide
clip = (VideoFileClip("birthday.mp4"))
clip.write_gif("birthday.gif")